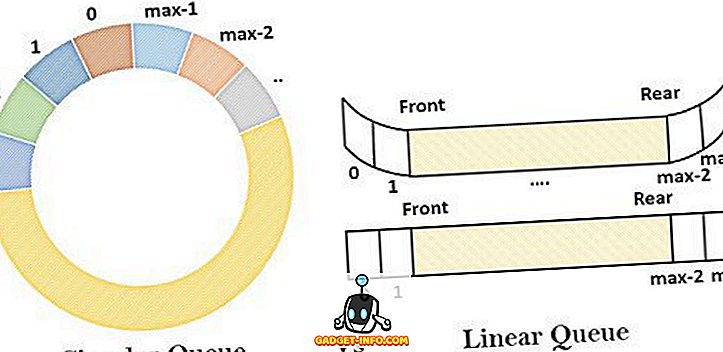
Die Warteschlange kann als nicht-primitive lineare Datenstruktur beschrieben werden, die der FIFO-Reihenfolge folgt, in der Datenelemente vom einen Ende (hinteres Ende) eingefügt und vom anderen Ende (vorderes Ende) gelöscht werden. Die anderen Varianten der Warteschlange sind die zirkuläre Warteschlange, die doppelt beendete Warteschlange und die Prioritätswarteschlange.
Vergleichstabelle
| Basis zum Vergleich | Lineare Warteschlange | Zirkulare Warteschlange |
|---|---|---|
| Basic | Ordnet die Datenelemente und Anweisungen in aufeinander folgender Reihenfolge an. | Ordnet die Daten in einem kreisförmigen Muster an, bei dem das letzte Element mit dem ersten Element verbunden ist. |
| Reihenfolge der Aufgabenausführung | Aufgaben werden in der Reihenfolge ausgeführt, in der sie zuvor platziert wurden (FIFO). | Die Reihenfolge der Ausführung einer Aufgabe kann sich ändern. |
| Einfügung und Löschung | Das neue Element wird von hinten hinzugefügt und von vorne entfernt. | Das Einfügen und Löschen kann an jeder Position erfolgen. |
| Performance | Ineffizient | Funktioniert besser als die lineare Warteschlange. |
Definition der linearen Warteschlange
Eine lineare Warteschlange ist rational eine First-in-First-Out- Order. Es wird linear genannt, weil es einer geraden Linie ähnelt, in der die Elemente hintereinander angeordnet sind. Es enthält eine homogene Sammlung der Elemente, in denen neue Elemente an einem Ende hinzugefügt und an einem anderen Ende gelöscht werden. Das Konzept der Warteschlange kann am Beispiel einer Warteschlange des Publikums verstanden werden, das vor dem Ticketschalter auf das Theaterticket wartet. In dieser Warteschlange schließt sich die Person am hinteren Ende der Warteschlange an, um das Ticket zu nehmen, und das Ticket wird am vorderen Ende der Warteschlange ausgegeben.
In der Warteschlange werden mehrere Vorgänge ausgeführt
- Zunächst wird die Warteschlange auf Null (dh leer) initialisiert.
- Stellen Sie fest, ob die Warteschlange leer ist oder nicht.
- Stellen Sie fest, ob die Warteschlange voll ist oder nicht.
- Einfügen des neuen Elements von hinten (Enqueue).
- Löschen des Elements vom Frontend (Dequeue).
Die Warteschlange kann auf zwei Arten implementiert werden
- Statisch (mit Arrays)
- Dynamisch (mit Zeigern)
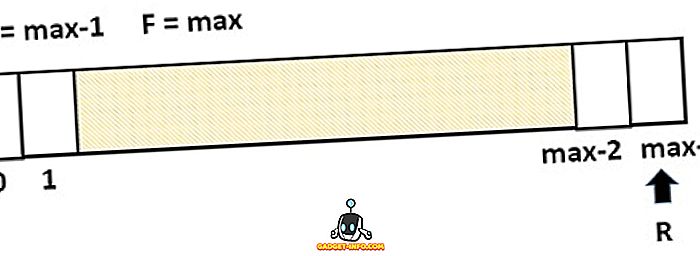
Die Einschränkung der linearen Warteschlange besteht darin, dass ein Szenario erstellt wird, in dem kein neues Element in die Warteschlange eingefügt werden kann, selbst wenn die Warteschlange leere Leerzeichen enthält. Diese Situation ist in der folgenden Abbildung dargestellt. Hier zeigt die Rückseite auf den letzten Index, während alle Felder noch leer sind und kein neues Element hinzugefügt werden kann.
Definition der zirkularen Warteschlange
Eine zirkuläre Warteschlange ist eine Variante der linearen Warteschlange, die die Begrenzung der linearen Warteschlange effektiv überwindet. In der kreisförmigen Warteschlange wird das neue Element an der ersten Position der Warteschlange hinzugefügt, wenn das letzte belegt ist und Platz verfügbar ist. Wenn es sich um eine lineare Warteschlange handelt, kann das Einfügen nur von hinten und das Löschen von vorne ausgeführt werden. In einer vollständigen Warteschlange entsteht nach einer Reihe aufeinanderfolgender Löschungen in der Warteschlange eine bestimmte Situation, in der kein neues Element hinzugefügt werden kann, selbst wenn der Platz verfügbar ist, da die Unterlaufbedingung (Rear = max - 1) noch besteht.
Die kreisförmige Warteschlange verbindet die beiden Enden durch einen Zeiger, wobei das allererste Element hinter dem letzten Element steht. Es verfolgt auch die Vorder- und Rückseite, indem es eine zusätzliche Logik implementiert, mit der die Elemente verfolgt werden können, die eingefügt und gelöscht werden sollen. Damit generiert die Umlaufwarteschlange die Überlaufbedingung erst dann, wenn die Warteschlange voll ist.
Einige Bedingungen, denen die zirkuläre Warteschlange folgt:
- Front muss auf das erste Element zeigen.
- Die Warteschlange ist leer, wenn Front = Rear ist.
- Wenn ein neues Element hinzugefügt wird, wird die Warteschlange um den Wert 1 erhöht (Rear = Rear + 1).
- Wenn ein Element aus der Warteschlange gelöscht wird, wird die Front um eins erhöht (Front = Front + 1).
Hauptunterschiede zwischen linearer Warteschlange und zirkularer Warteschlange
- Die lineare Warteschlange ist eine geordnete Liste, in der Datenelemente in der sequentiellen Reihenfolge organisiert sind. Im Gegensatz dazu speichert die Warteschlange die Daten kreisförmig.
- Die lineare Warteschlange folgt der FIFO-Reihenfolge für die Ausführung der Task (das an der ersten Position hinzugefügte Element wird an der ersten Position gelöscht). Umgekehrt kann sich in der kreisförmigen Warteschlange die Reihenfolge der für ein Element ausgeführten Operationen ändern.
- Das Einfügen und Löschen der Elemente wird in der linearen Warteschlange festgelegt, dh Hinzufügen vom hinteren Ende und Löschen vom vorderen Ende. Andererseits kann die kreisförmige Warteschlange das Element von einem beliebigen Punkt aus einfügen und löschen, bis es unbesetzt ist.
- Bei einer linearen Warteschlange wird Speicherplatz verschwendet, während bei der kreisförmigen Warteschlange Speicherplatz effizient genutzt wird.
Implementierung der linearen Warteschlange
Der unten angegebene Algorithmus veranschaulicht das Hinzufügen von Elementen in einer Warteschlange:
Die Warteschlange benötigt drei Datenvariablen, darunter ein Array zum Speichern der Warteschlange und andere, um die vordere und hintere Anfangsposition (-1) zu speichern.
einfügen (Artikel, Warteschlange, n, hinten) {if (hinten == n), dann "Warteschlangenüberlauf" ausgeben; sonst {hinten = hinten + 1; Warteschlange [Hinten] = Artikel; }} Der unten angegebene Algorithmus veranschaulicht das Löschen von Elementen in einer Warteschlange:
delete_circular (Artikel, Warteschlange, hinten, vorne) {wenn (hinten == vorne), dann "Warteschlangenunterlauf" drucken; else {front = front + 1; item = Warteschlange [Vorderseite]; }} Implementierung der zirkularen Warteschlange
Ein Algorithmus zum Interpretieren des Hinzufügens des Elements in der zirkularen Warteschlange:
insert_circular (Artikel, Warteschlange, hinten, vorne) {hinten = (hinten + 1) mod n; wenn (vorne == hinten) dann "Warteschlange ist voll" drucken; else {Warteschlange [hinten] = item; }} Der Algorithmus erklärt das Löschen des Elements in der zirkularen Warteschlange:
delete_circular (Artikel, Warteschlange, hinten, vorne) {wenn (vorne == hinten), dann drucken ("Warteschlange ist leer"); else {front = front + 1; item = Warteschlange [Vorderseite]; }} Fazit
Die lineare Warteschlange ist in bestimmten Fällen ineffizient, in denen die Elemente in die leeren Räume verschoben werden müssen, um einen Einfügevorgang durchzuführen. Aus diesem Grund wird der Speicherplatz häufig verschwendet, während die ringförmige Warteschlange den Speicherplatz angemessen nutzt, da die Elemente an einer beliebigen Position hinzugefügt werden, wenn ein leerer Speicherplatz vorhanden ist.