Sortieren ist eine grundlegende Operation, bei der die Elemente eines Arrays in einer bestimmten Reihenfolge angeordnet sind, um die Suchbarkeit zu verbessern. In einfachen Worten werden die Daten so sortiert, dass sie leicht durchsucht werden können.
Vergleichstabelle
| Basis zum Vergleich | Sortieren durch Einfügen | Auswahl sortieren |
|---|---|---|
| Basic | Die Daten werden sortiert, indem die Daten in eine vorhandene sortierte Datei eingefügt werden. | Die Daten werden sortiert, indem die aufeinanderfolgenden Elemente ausgewählt und an einem sortierten Ort platziert werden. |
| Natur | Stabil | Instabil |
| Prozess zu folgen | Elemente sind vorab bekannt, während der Ort, an dem sie platziert werden sollen, gesucht wird. | Der Ort ist bereits bekannt, während Elemente gesucht werden. |
| Sofortige Daten | Einfügungssortierung ist eine Live-Sortiertechnik, die unmittelbare Daten verarbeiten kann. | Es kann nicht mit sofortigen Daten umgehen, es muss am Anfang vorhanden sein. |
| Bester Fall Komplexität | Auf) | O (n 2 ) |
Definition der Einfügung Sort
Die Einfügungssortierung funktioniert durch Einfügen des Wertesatzes in die vorhandene sortierte Datei. Das sortierte Array wird erstellt, indem jeweils ein einzelnes Element eingefügt wird. Dieser Vorgang wird fortgesetzt, bis das gesamte Array in einer bestimmten Reihenfolge sortiert ist. Das Hauptkonzept hinter der Einfügungssortierung ist das Einfügen jedes Elements an der entsprechenden Stelle in der endgültigen Liste. Die Einfüge-Sortiermethode spart effektiv Speicherplatz.
Arbeit der Einfügungsart
- Es verwendet zwei Gruppen von Arrays, in denen eine die sortierten Daten und die anderen die unsortierten Daten speichert.
- Der Sortieralgorithmus funktioniert, bis Elemente im unsortierten Satz vorhanden sind.
- Nehmen wir an, es gibt n Elemente im Array. Anfangs ist das Element mit dem Index 0 (LB = 0) in der sortierten Menge vorhanden. Die restlichen Elemente befinden sich in der unsortierten Partition der Liste.
- Das erste Element des unsortierten Teils hat den Feldindex 1 (If LB = 0).
- Nach jeder Wiederholung wählt es das erste Element der unsortierten Partition aus und fügt es an der richtigen Stelle im sortierten Satz ein.
Vorteile der Einfügungsart
- Einfach zu implementieren und sehr effizient, wenn kleine Datenmengen verwendet werden.
- Der zusätzliche Speicherplatzbedarf für die Einfügungssortierung ist geringer (dh O (1)).
- Es handelt sich um eine Live-Sortierungstechnik, da die Liste beim Empfang der neuen Elemente sortiert werden kann.
- Es ist schneller als andere Sortieralgorithmen.
Beispiel:
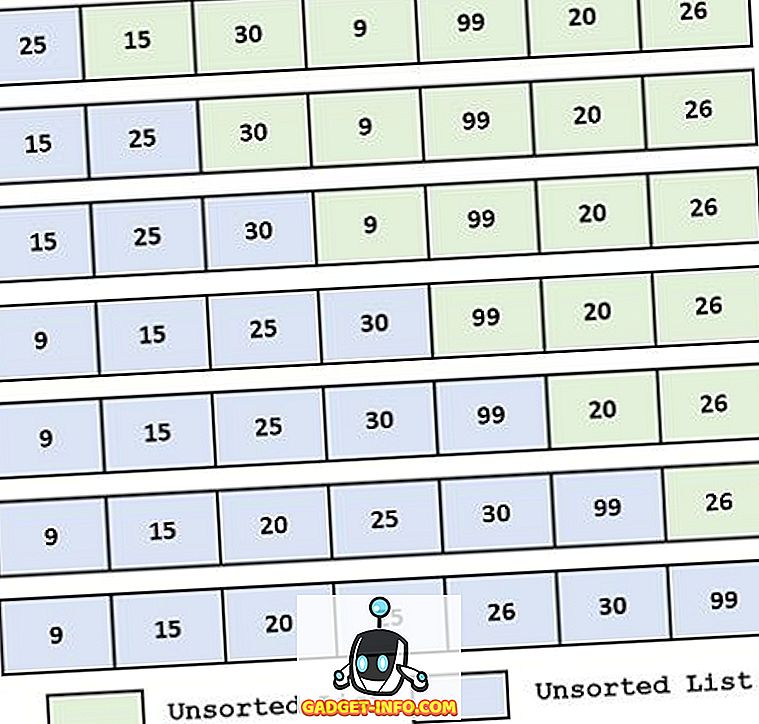
Definition der Auswahl Sort
Die Auswahl Sortierung führt eine Sortierung durch, indem nach der Mindestwertnummer gesucht und entsprechend der Reihenfolge (aufsteigend oder absteigend) an der ersten oder letzten Position platziert wird. Der Suchvorgang des Mindestschlüssels und das Platzieren an der richtigen Position wird fortgesetzt, bis alle Elemente an der richtigen Position platziert sind.
Arbeitsweise der Auswahlsortierung
- Angenommen, ein Array ARR mit N Elementen im Speicher.
- Im ersten Durchlauf wird der kleinste Schlüssel zusammen mit seiner Position gesucht, dann wird ARR [POS] mit ARR [0] ausgetauscht. Daher wird ARR [0] sortiert.
- Im zweiten Durchlauf wird wiederum die Position des kleinsten Wertes im Unterfeld von N-1 Elementen bestimmt. Tauschen Sie ARR [POS] mit ARR [1] aus.
- In dem Durchlauf N-1 wird derselbe Vorgang ausgeführt, um die Anzahl der N Elemente zu sortieren.
Beispiel:
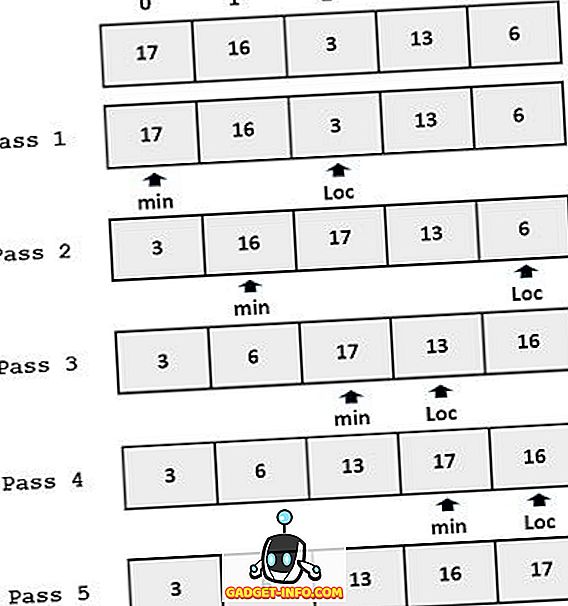
Hauptunterschiede zwischen Einfügungssortierung und Auswahlsortierung
- Die Einfügesortierung führt normalerweise den Einfügevorgang aus. Im Gegensatz dazu führt die Auswahlsortierung die Auswahl und Positionierung der erforderlichen Elemente durch.
- Einfügesortierung gilt als stabil, während Auswahlsortierung kein stabiler Algorithmus ist.
- Beim Einfügungssortieralgorithmus sind die Elemente vorbekannt. Im Gegensatz dazu enthält die Auswahlsortierung zuvor den Ort.
- Einfügungssortierung ist eine Live-Sortierungsmethode, bei der die ankommenden Elemente sofort in der Liste sortiert werden, während die Auswahlsortierung mit Direktdaten nicht gut funktioniert.
- Die Einfügungssortierung hat im besten Fall die Laufzeit von O (n). Im Gegensatz dazu ist die Laufzeitkomplexität der Auswahlsortierung im besten Fall O (n2).
Komplexität der Einfügungsart
Die beste Komplexität der Einfügungssortierung ist O (n) mal, dh wenn das Array zuvor sortiert wurde. Auf dieselbe Weise ist, wenn das Array in umgekehrter Reihenfolge sortiert wird, das erste Element des unsortierten Arrays mit jedem Element in der sortierten Menge zu vergleichen. Im ungünstigsten Fall ist die Laufzeit der Insertion-Sorte also quadratisch, dh O (n2) . Im Durchschnittsfall müssen auch die Mindestvergleiche (k-1) / 2 durchgeführt werden. Daher hat der Durchschnittsfall auch eine quadratische Laufzeit O (n2).
Komplexität der Auswahlsortierung
Bei der Auswahl der Auswahl hängt die Sortierung nicht von der ursprünglichen Reihenfolge der Elemente im Array ab. Daher besteht kein großer Unterschied zwischen der Best-Case-Komplexität und der Worst-Case-Komplexität der Auswahlsortierung.
Die Auswahlsortierung wählt das Element mit dem minimalen Wert aus. Im Auswahlprozess werden alle 'n' Elemente durchsucht. Daher werden im ersten Durchgang n-1-Vergleiche durchgeführt. Dann werden die Elemente ausgetauscht. Um das zweite kleinste Element zu finden, müssen wir ebenfalls die restlichen n-1-Elemente scannen, und der Vorgang wird fortgesetzt, bis das gesamte Array sortiert ist.
Somit ist die Laufzeitkomplexität der Auswahlsortierung O (n2) .
= (n-1) + (n-2) + ……… .. + 2 + 1
= n (n-1) / 2 = O (n2)
Fazit
Bei beiden Sortieralgorithmen ist die Einfügungssortierung schnell, effizient und stabil, während die Auswahlsortierung nur dann effizient arbeitet, wenn der kleine Satz von Elementen betroffen ist oder die Liste teilweise zuvor sortiert ist. Die Anzahl der durch die Auswahlsortierung vorgenommenen Vergleiche ist größer als die durchgeführten Bewegungen, während bei der Einfügungssortierung die Anzahl der Verschiebungen oder Auslagerungen eines Elements größer ist als die durchgeführten Vergleiche.